What is Throttling?
Throttling is a technique that limits how many times a function can be called in a specific period of time. It improves the speed and responsiveness of web sites by implementing event listeners that do heavy or expensive tasks such as animations, scrolling, resizing, getting data, etc.
For example, if you have a function that collects data from an API every time the user scrolls down the page, you can throttle it so that it only makes one request per second instead of hundreds as the user scrolls. This prevents you from overloading the server or browser with unnecessary queries, hence reducing bandwidth usage.
Why use Throttling in JavaScript?
JavaScript Throttling can increase application performance by setting a set rate of function execution.
A Throttle function generates function calls at predefined intervals, keeping the program from lagging or becoming overloaded. As a result the server will handle requests in a certain order and at a predetermined time.
Implement Throttling in JavaScript
Here are the steps you can follow to create Throttling in JavaScript −
- Create a Throttle Function: Define a function that accepts a callback and a delay to adjust the execution frequency over time.
- Track Last Run Time: Save the timestamp from the last function called to see if the wait has been completed.
- Check Time Interval: For each trigger, compare the current time to the last execution time; execute only if enough time has passed.
- Return the Throttled Function: Create a new function that only executes the old callback when the specified time period is met.
How Throttling work in JavaScript?
Let us look at an example to better understand JavaScript and throttling. Consider this scenario: we have added a scroll event listener to a web page and configured it such that when the user scrolls, he sees the desired information.
But if the user scrolls frequently, the web page will soon generate hundreds of events. To address this issue, we will throttle the event so that it is only triggered after a second of the previous event. This results in a single callback every second. The end user will see the same results, but they will be far more computationally efficient.
Now Let us understand it with the help of the example below. In the following example, we will use the throttle mechanism to distinguish between throttling and non-throttling conditions.
Without throttling Function
Without throttling, a function can be called too quickly, causing performance issues, excessive resource usage and a possibly unpleasant user experience.
Example
In this example, we add an event listener to a button without throttling. Each click triggers the callback immediately and sending the message ‘button is clicked’ to the console with no rate limit.
<!DOCTYPE html><html lang="en"><head><meta charset="UTF-8"><meta name="viewport"
content="width=device-width,
initial-scale=1.0"><title>Document</title></head><body><button id="pressButton">Press Me</button><script>
// Selected button with the given id
const button = document.
querySelector("#pressButton");
// Add event listener to the button
// to listen to the click event
button.addEventListener("click", () => {
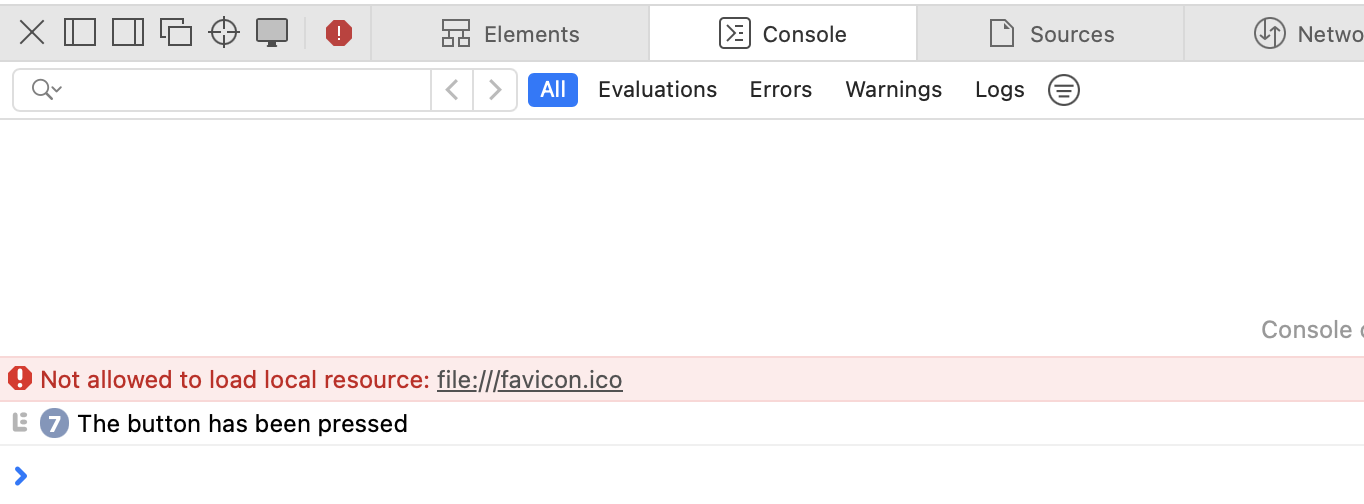
console.log("The button has been pressed");
});
</script></body></html>
Output
This will produce the below result −
With Throttling Function
Throttling limits the number of function invocations. For example, you could choose to execute a function at most once per 1500 milliseconds. This prevents the function from being called too frequently, which results in smoother performance.
Example
In this example we throttle a button click event by limiting the ‘Button has been pressed!’ log to once per 1500 milliseconds, regardless of how quickly we click.
Following is the simple demonstration with throttling function −
<!DOCTYPE html><html lang="en"><head><meta charset="UTF-8"><meta name="viewport"
content="width=device-width,
initial-scale=1.0"><title>Document</title></head><body><button id="pressButton">Press Me</button><script>
const button = document.querySelector("#pressButton");
// Throttling Function
const limitFunctionCall = (callback, waitTime) => {
// Previously called time of the function
let lastCalled = 0;
return (...args) => {
// Current called time of the function
let currentTime = new Date().getTime();
// Logging the difference
// between previously called and current called timings
console.log("Time difference:", currentTime - lastCalled, "Wait time:", waitTime);
// If the difference is greater than waitTime, call the function again
if (currentTime - lastCalled > waitTime) {
lastCalled = currentTime;
// Return the function
return callback(...args);
}
}
}
button.addEventListener("click",
limitFunctionCall(() => {
console.log("Button has been pressed!")
}, 1500));
</script></body></html>
Output
This will generate the below result −
[Log] Time difference: - 1729667433711 - "Wait time:" - 1500 (example.html, line 28) [Log] Button has been pressed! (example.html, line 41) [Log] Time difference: - 1016 - "Wait time:" - 1500 (example.html, line 28) [Log] Time difference: - 1599 - "Wait time:" - 1500 (example.html, line 28) [Log] Button has been pressed! (example.html, line 41) [Log] Time difference: - 416 - "Wait time:" - 1500 (example.html, line 28) [Log] Time difference: - 866 - "Wait time:" - 1500 (example.html, line 28)
Use cases for Throttling
A throttle function operates at a fixed rate to prevent the app from lagging or overwhelming the server when performing a time-consuming task or request. The following are some common applications for the throttle function.
- In Gaming: In games, players press buttons to perform actions like punching and shooting. If they press too quickly we can use throttle to limit the frequency of activities like once per second.
- Ads and Scrolling: When users scroll we regularly load and animate content. Scrolling too quickly can lead to the app to slow down. Throttling keeps things functioning smoothly by limiting actions.
- Button Clicks:Some programs, like those used at ATMs, take longer to complete tasks. Throttling prevents users from pressing the button too quickly.
- Pointer (Mouse) Events:Moving the mouse can lead to events to occur too frequently. Throttling controls how frequently these events occur to ensure that everything runs properly.
- API Calls: If an app makes too many API requests quickly it can slow down loading. Throttling limits requests to prevent problems.
Summary
JavaScript Throttling is an approach that restricts function execution to a specific number of times. It ensures that a function is executed on a consistent basis, regardless of how many times it has been invoked.
